אוג'
03
2011
קבצים מצורפים: היחידה כקובץ PDF, מצגת PPT
השוואה בין גורמים שונים היא חלק מחיי היומיום שלנו. במתמטיקה השוואות מתורגמות למשוואות ולאי-שוויונות המקבלים ייצוגים שונים: מילולי, גרפי, מספרי, ואלגברי.
בפתרון שאלה מילולית המתארת השוואה, נדרשת אוריינות מתמטית. הפותר צריך להבין את הנקרא, ולדעת לתרגם את התיאור המילולי לייצוג מתמטי אחר (גרפי, מספרי או אלגברי) אשר יוביל לתשובה.
התמודדות עם שאלות מילוליות המתארות אי-שוויון, דורשת הבנה של דקויות מילוליות. אוצר המונחים הלשוניים המתארים מצבי אי-שוויון רבים ומגוונים. ההבדלים הדקים בין מושגי האי-שוויון דורשים הבנה מעמיקה של הטקסט. למשל, המשפט "לדני יש 8 גולות לכל היותר" מתורגם ל-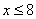
והמשפט "לדני יש יותר מ-8 גולות" מתורגם ל- 
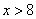. ה"כיוון" של סימן האי-שוויון שונה וגם האי-שוויון הראשון הוא אי-שוויון חלש (מאפשר גם את השוויון עצמו) בעוד השני הוא אי-שוויון חזק (אינו מאפשר את השוויון עצמו).
ביחידה זו נתמקד במשמעות הלוגית של אי-שוויון ובפתרון שאלות מילוליות המתארות אי-שוויון:
- נעסוק בדקויות ההבחנה בין המונחים המתארים אי-שוויונות.
- נבדיל בין מונחים המאפשרים שימוש באי-שוויון חלש או חזק.
- בפתרון השאלות נשתמש, במידת האפשר, בדרכים שונות ובייצוגים מגוונים.
אוג'
03
2011
או מדוע "מינוס כפול מינוס שווה פלוס"?
קבצים מצורפים: היחידה כקובץ PDF
פעולת הכפל במספרים השליליים היא פעולה המוגדרת באופן מתמטי פורמלי ולאו דוקא אינטואיטבי. זו אחת הפעולות הראשונות שפוגש התלמיד בבית הספר שמקורן אינו בהתנסויות מוחשיות ואינטואיטיביות. השרירותיות של החוקים המתמטיים מהווה לעיתים אבן נגף ברצף הלמידה של הרחבת המספרים וראשית האלגברה.
ביחידה זו נבחן הסברים שונים המקובלים בהוראה, בכדי להצדיק את חוקי הכפל במספרים השליליים ובפרט מדוע כפל של שני מספרים שליליים הוא חיובי. הצגת המספרים השליליים ופעולות החיבור והחיסור בהם נלמדות בדרך כלל בתווך של מודלים דידקטיים כגון חיצים על ציר המספרים, מודל האסימונים וכדומה (ראו סקירה נרחבת ביחידה "להיות מודל למספר שלילי"). ביחידה זו נשאל האם וכיצד נמשיך להשתמש במודלים להוראת פעולת הכפל במספרים שליליים וכן אילו אסטרטגיות מתאימות להצגת פעולת הכפל במספרים השליליים.
יחידה זו עוקבת ליחידה "להיות מודל למספר שלילי", אך יכולה לעמוד גם בפני עצמה.
אוג'
03
2011
מודלים שונים להצגת המספרים השליליים ופעולות החיבור והחיסור בהם
קבצים מצורפים: היחידה כקובץ PDF
היחידה עוסקת בחשיפה למודלים שונים המשמשים להוראת המספרים השלמים, השוואה בין המודלים השכיחים ובחינת המשמעות של המספר השלילי ופעולות החיבור והחיסור בכל אחד מהמודלים.
הנושאים המרכזיים
- הרחבת עולם המספרים.
- מספר שלילי – מהו?
- מושגים מרכזיים בהגדרת המספר השלילי – האפס, היחידה, נגדיות, סדר וצפיפות.
- ייצוגים שונים של המספרים השליליים במגוון מודלים דידקטיים.
- מה בין מושג ומודל?
- ארבע פעולות החשבון והמשמעות שלהן במודלים השונים.
- מקומם של המודלים בהוראה: נקודות חוזק ותורפה.
אי-שוויונות בשאלות מילוליות
