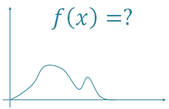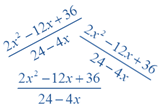דצמ'
21
2011
קבצים מצורפים: היחידה כקובץ PDF
נושא המרובעים הינו אחד הנושאים המרכזיים בתוכנית הלימודים בגיאומטריה לכיתה ט'. בהתאם לתוכנית הלימודים לכיתה ט' נלמד נושא זה בגישה דדוקטיבית תוך שימת דגש על הגדרות מושגים, משפטים מתמטיים והוכחתם. הגישה הננקטת להוראת נושא זה כפי שהיא באה לידי ביטוי בתוכנית הלימודים החדשה מתחילה בהוראת המקבילית דרך המלבן (מרובע אותו למדו התלמידים בכיתה ז' והוגדר כמרובע בעל ארבע זויות ישרות), המעוין, הריבוע, הדלתון והטרפז כלומר ההוראה מתבצעת בדרך של "הורדה" של חלק מהתנאים המספיקים שנכללים בהגדרת המרובע, והוספת תנאים הכרחיים למושג.
היחידה מתייחסת להיבטים מתמטיים ודידקטיים הקשורים למבנה המשפט המתמטי והגדרת המושג. היחידה מעודדת:
- הכרות עם גישות שונות (מתמטיות ודידקטיות) להוראת משפחת המרובעים.
- הכרות עם ריבוי ההגדרות ושקילות טענות מתמטיות היכולות לשמש כהגדרות לאותו מושג.
- דיון בהיבטים מתה-מתמטיים הממוקדים בבחירת "ההגדרה הטובה".
- דיון על האופן בו משפיעה בחירת ההגדרה על סדר הוראת המושגים.
- הכרות עם נושא הסימטריה (סימטריה שקופית ומרכזית מהוות חלק מהנושאים הנדרשים במבחן הטימס) והשימוש בסימטריה בהגדרת בנושא המרובעים.
דצמ'
21
2011
קבצים מצורפים: היחידה כקובץ PDF
טרנספורמציות הן כלי מתמטי ליצירת משפחה של פונקציות. הן מעודדות להסתכל על הפונקציה כדוגמה או כפרט במשפחה. "חוש לפונקציות" כולל גם את היכולת לשייך פונקציה למשפחה שלה ולזהות את התכונות המשותפות למשפחה (Confrey, 1994) והטרנספורמציות הן כלי לנוע בין הפונקציות בתוך המשפחה.
תלמיד שפיתח יכולות להבין ולדמיין טרנספורמציות על פונקציות בייצוגן הגרפי והאלגברי ומזהה פונקציה כשייכת למשפחה, יוכל להשתמש בטרנספורמציות ככלי שימושי כמעט בכל נושא הנוגע לפונקציות, כגון הכרות עם משפחות שונות של פונקציות, נגזרות, מניפולציות אלגבריות ועוד.
נעסוק כאן בארבעה סוגים יסודיים של טרנספורמציות לינאריות:
- הזזה אנכית
- הזזה אופקית
- מתיחה אנכית
- מתיחה אופקית
- שיקופים.
דצמ'
18
2011
קבצים מצורפים: היחידה כקובץ PDF
עיסוק במצולעים בעלי יותר מ- 4 צלעות, פותח אפשרויות להצגת משולשים ומרובעים כמקרים פרטיים של מצולעים (כלליים) ויכול להוביל להעמקה והרחבה של מושגים ותכונות רבות כמו אלכסונים, זוויות פנימיות וחיצוניות במצולע, מצולע משוכלל, סכום זוויות במצולע וכדומה. עיסוק במושג "המצולע" מאפשר שילוב של פעולות חקר בשיעורי מתמטיקה, פותח אפשרויות לשאלת שאלות, להעלאת השערות, מוביל להכללות והוכחות.
רב המשימות ביחידה יכולות לשמש דוגמה להוראה קדם דדוקטיבית בגיאומטריה.
מטרות היחידה: העמקה במושגי יסוד הקשורים במצולעים בדרך חווייתית, הצגת דוגמה ללמידת מושג מתוך דוגמאות מתאימות, הצגת דוגמה ללימוד בדרכי חקר.
יחידה זאת מעשירה מורים בנושא הנחשב מוכר. הפעילויות בנויות בצורת בעיות חקר דבר המעודד הוראה הדרגתית ומאפשר הוראה לא-פרונטאלית. היחידה ניתנת ברובה ליישום בכתות, היא מתאימה לכל קבוצת גיל ואפשר לשלב חלקים ממנה ברמות שונות.
דצמ'
18
2011
קבצים מצורפים: היחידה כקובץ PDF
היחידה מציגה את הפונקציה הריבועית בייצוגים סימבוליים שונים ובייצוג הגרפי (פרבולה).
היחידה מדגישה את היתרונות של כל הצגה סימבולית, תוך שימוש ביישומים דינאמים לפעילות חקר על הקשר והאיכויות של כל הצגה.
בשנות השמונים רווחה התיאוריה הקונסטרוקטיביסטית להוראת המתמטיקה עיקר תיאוריה זו היא שהלמידה היא תהליך פנימי, בו הלומד בונה ידע חדש על בסיס הבנייה אישית של הלומד מתוך ידע קיים. לכן, חשוב שלימוד המתמטיקה יביא ליצירת קשר בין הידע הנרכש לבין הידע הקיים.
סדנה אחת עוסקת בבניית פונקציה ריבועית כמכפלה של שתי פונקציות לינאריות. הפונקציות הלינאריות מוכרות לתלמידים, וממכפלתם, ניתן ללמוד על רב התכונות של הפונקציה הריבועית.
ויתר הסדנאות עוסקות בדגשים של הייצוגים הסימבוליים השונים ובמשפחות של פונקציות.
דצמ'
18
2011
קבצים מצורפים: היחידה כקובץ PDF
"מושג הפונקציה מאפשר ארגון ומיזוג של רעיונות מתמטיים חשובים ובעלי משמעות עבור התלמידים" (מתוך תוכנית הלימודים של חטיבת הביניים).
יחידה זו מציגה מבוא כללי למושג הפונקציה שהוא מושג בסיסי בלימודי המתמטיקה השזור לאורך כל תוכנית הלימודים בחטיבת הביניים ובחטיבה העליונה. יחידה זו כוללת רקע מתמטי, היסטורי ודידקטי גם עבור היחידות:
- פונקציה ריבועית
- טרנספורמציות ליניאריות
דצמ'
18
2011
קבצים מצורפים: היחידה כקובץ PDF
מטרת היחידה – בניית ייצוגים גיאומטריים להוכחות של זהויות אלגבריות ופיתוח יכולת הבניית מושגים בצורה עצמאית.
כיום, בעידן המחשבים, הולכת וגוברת ההכרה בכך שלייצוגים ויזואליים יש פוטנציאל העשוי לתרום לתהליך הלמידה, להעשיר אותו, ולהביא להבנה מעמיקה של מושגים מתמטיים.
דצמ'
18
2011
קבצים מצורפים: היחידה כקובץ PDF
יחידה זו עוסקת במיומנויות נדרשות בטכניקה אלגברית בשילוב של דרכי חשיבה שונות.
ביחידה זו נעסוק במיומנויות הבאות:
1. כינוס איברים דומים
2. פתיחת סוגריים (חוק הפילוג וחוק הפילוג המורחב)
3. נוסחאות לכפל מקוצר
4. פירוק לגורמים בשיטות שונות: הוצאת גורם משותף מחוץ לסוגריים, קיבוץ איברי הפולינום, פירוק של טרינום ריבועי
5. הרחבה וצמצום של שברים אלגבריים
6. מציאת מכנה משותף של שברים אלגבריים הנדרש לביצוע חיבור וחיסור שלהם
7. כפל וחילוק של שברים אלגבריים
8. שימוש בחוקי חזקות וחוקי השורש הריבועי
נוב'
16
2011
בגרסה הראשונה של האוגדן, אשר הודפסה וחולקה לכם הופיעו מספר טעויות ואי-דיוקים.
אנו מפרסמים רשימת תיקונים. מומלץ לתקן ידנית בגרסתכם, או להדפיס מחדש את עמודים הרלוונטיים.
שימו לב: מספרי העמודים בטבלה מתאימים למספרי העמודים של גרסת האוגדן שבידיכם. בגרסה הנמצאת באתר (אשר כבר כוללת את כל התיקונים), מספרי העמודים יכולים להיות שונים מעט.
רשימת תיקונים בקובץ PDF
|
שם היחידה
|
עמוד
|
תיקון
|
|
כפל של מספרים שליליים
|
9
|
בעמודה השמאלית בטבלה צריך להופיע "2+" במקום "2-".
פורסם בתאריך 27.11.11
|
|
שטחים – יחידה 3 -
השטח במבט מודרני
|
שער
|
"יחידה 3", ולא "יחידה 2".
אפשר גם להחליף את הסדר הפיזי בין יחידה 2 ויחידה 3 בתוך האוגדן, אם הסדר לא נכון.
פורסם בתאריך 27.11.11
|
| |
5, 9
|
בנוסחת חיבור השטחים, צריך להופיע סימן איחוד (∪) במקום סימן חיתוך (∩) בפעם השנייה. הנוסחה הנכונה:
<= ![clip_image001[16] clip_image001[16]](http://highmathbb.haifa.ac.il/wp-content/uploads/2011/11/clip_image001161.gif) = (Area(P1∩P2 = (Area(P1∩P2
(Area(P1∪P2) = Area(P1) + Area(P2
פורסם בתאריך 27.11.11
|
|
הסתברות – החוקיות של האי ודאות
|
12
|
שאלה 2, סעיף ב' – הפתרון צריך להיות:
פתרון: את הוצאת כל עשרים וחמישה התפוחים מהארגז ניתן לראות כסידור של כל התפוחים בשורה אחת (המספר הכולל של שורות אלה שווה ל- 25!).
ההסתברות לקבלת כל אחת משורות אלו שווה.
מספר השורות שבהם התפוח הירוק מופיע במקום הראשון שווה למספר השורות שבהם התפוח הירוק מופיע במקום השלישי.
הערה: הסבר זה מהווה דרך אלטרנטיבית לדרך הפתרון המוצגת בדרך כלל לתלמידים בעזרת דיאגרמת עץ. במקרה והשאלה מתייחסת למשל, לתפוח השלישי, הסבר זה לא בהכרח קל ונח יותר מאשר הדרך הקונוונציונלית. יתרון הסבר זה בכך בהצגת חשיבה הנכונה גם כאשר מדובר למשל, על התפוח ה-23.
פורסם בתאריך 27.11.11
|
| |
18
|
שאלה 4 – סעיף ג, פתרון בדרך ב – דיאוגרמת עץ – לפני המשפט האחרון בפתרון יש להוסיף:
כיוון ש- ![clip_image003[5] clip_image003[5]](http://highmathbb.haifa.ac.il/wp-content/uploads/2011/11/clip_image00351.gif) ומכאן, ומכאן, ![clip_image005[5] clip_image005[5]](http://highmathbb.haifa.ac.il/wp-content/uploads/2011/11/clip_image00551.gif) ולכן, ערך הביטוי ולכן, ערך הביטוי![clip_image007[5] clip_image007[5]](http://highmathbb.haifa.ac.il/wp-content/uploads/2011/11/clip_image00751.gif) גדול מערד הביטוי גדול מערד הביטוי ![clip_image009[5] clip_image009[5]](http://highmathbb.haifa.ac.il/wp-content/uploads/2011/11/clip_image00951.gif) . .
פורסם בתאריך 27.11.11
|
| |
19
|
שאלה 4 – סעיף ג, פתרון בדרך ג – דיאוגרמת עץ:
מומלץ להחליף את שמות ההרכבים א ו-ב ל-A ו-B בהתאמה, לתיאום עם הפתרונות בהמשך.
פורסם בתאריך 27.11.11
|
| |
19
|
שאלה 4 – סעיף ד: - התשובה המלאה היא:
תשובה: לא משנה על איזה הרכב נמליץ. ההסתברות ששלושה שופטים יקבלו החלטה נכונה או ארבעה שופטים יקבלו את ההחלטה הנכונה שווה.
פורסם בתאריך 27.11.11
|
| |
19, 20
|
בתרשים
במקרה האמצעי צריך להיות כתוב "שלושה שופטים החליטו החלטה נכונה ואחד שגה"
פורסם בתאריך 27.11.11
|
| |
20
|
שאלה 4 – סעיף ד – הוספנו עוד דרך לפתרון:
פתרון בדרך ב': דרך איכותית
נתבונן במצב הבא:
בהרכב B מבין ארבעת השופטים, שופט IV מביע את דעתו, אך "מתעלמים" ממנו. הרכב זה יקבל החלטות בהסתברות שווה להסתברות שהרכב של שלושה שופטים יקבל החלטה נכונה.
נשווה את הרכבB להרכב A בו מתחשבים בדעות של כל אחד מארבעת השופטים. (כלומר, לא מתעלמים מאף אחד). אם 3 שופטים מתוך 4 קיבלו החלטה נכונה, אז בשני ההרכבים ההחלטה הנכונה תהיה זהה (בהרכב B, אפילו אם בין שלושת האלה יהיה שופט IV, בכל זאת הרוב בעד ההחלטה הנכונה).
אם בדיוק 2 קיבלו החלטה נכונה ("תיקו"), אז בשני ההרכבים ההחלטה הנכונה תתקבל במחצית מהמקרים: בהרכב A מטילים מטבע ובהרכב B בחצי מהמקרים שופט IV נמצא בזוג שמקבל החלטה נכונה (ראה שאלה מספר 3).
לכן ההסתברות שהרכב A יקבל החלטה נכונה שווה לזו שהרכב B יקבל את ההחלטה הנכונה.
הערות:
1. שימו לב, שעל מנת להשוות בין הסתברויות לא חייבים לחשב אותם.
2. בדומה לפתרון בדרך B ניתן לראות כי אין הבדל בין הסתברויות של הרכב שבו 2n–1 שופטים להרכב שבו 2n שופטים.
פורסם בתאריך 27.11.11
|
אם גיליתם טעויות נוספות – אנא יידעו אותנו.
אוג'
07
2011
קיבוץ לביא – 17.7.2011 – 19.7.2011
היקף – 30 שעות
המצגות כולן לשימוש המדריכים. אנא הקפידו על שמירת זכויות היוצרים וציינו את מקורן.
אוג'
03
2011
קבצים מצורפים: היחידה כקובץ PDF, מצגת PPT
יחידה זו מציגה ארבע בעיות בהסתברות שעשויות לפתח חשיבה הסתברותית וחשיבה ביקורתית.
כיום, בעולם המודרני, השימוש במונחי הסתברות הולך וגובר, אם בהתנסחויות התקשורתיות בתחומי החיים השונים ואם בשפת היומיום. לכן חשוב לבסס אצל התלמידים עולם מושגים הסתברותיים, לפתח יכולת ניתוח בעיות הסתברותיות וכושר ביקורת להצהרות הסתברותיות.
לכל אחד מאיתנו יש אינטואיציה לגבי סיטואציות יומיומיות בלתי ודאיות בחיינו, אך לא תמיד הן מתיישבות עם תורת ההסתברות. קיום הסתירה לכאורה בין מדע ההסתברות לבין החשיבה ההגיונית שלנו, משאיר אותנו לעתים עם גורם ההפתעה בקשר לתשובה החישובית. בפעילות ביחידה זו נראה שחישובי ההסתברויות לא תמיד עולים בקנה אחד עם שיקול הדעת האינטואיטיבי שלנו לגבי סיטואציות הסתברותיות. יחד עם זאת נראה שניתן לפתח חשיבה איכותנית ולוגית לפתרון הבעיות, ללא חישובים, יחד עם ייצוגים מגוונים המסייעים להבנת הבעיות.