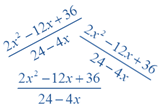דצמ'
18
2011
קבצים מצורפים: היחידה כקובץ PDF
מטרת היחידה – בניית ייצוגים גיאומטריים להוכחות של זהויות אלגבריות ופיתוח יכולת הבניית מושגים בצורה עצמאית.
כיום, בעידן המחשבים, הולכת וגוברת ההכרה בכך שלייצוגים ויזואליים יש פוטנציאל העשוי לתרום לתהליך הלמידה, להעשיר אותו, ולהביא להבנה מעמיקה של מושגים מתמטיים.
דצמ'
18
2011
קבצים מצורפים: היחידה כקובץ PDF
יחידה זו עוסקת במיומנויות נדרשות בטכניקה אלגברית בשילוב של דרכי חשיבה שונות.
ביחידה זו נעסוק במיומנויות הבאות:
1. כינוס איברים דומים
2. פתיחת סוגריים (חוק הפילוג וחוק הפילוג המורחב)
3. נוסחאות לכפל מקוצר
4. פירוק לגורמים בשיטות שונות: הוצאת גורם משותף מחוץ לסוגריים, קיבוץ איברי הפולינום, פירוק של טרינום ריבועי
5. הרחבה וצמצום של שברים אלגבריים
6. מציאת מכנה משותף של שברים אלגבריים הנדרש לביצוע חיבור וחיסור שלהם
7. כפל וחילוק של שברים אלגבריים
8. שימוש בחוקי חזקות וחוקי השורש הריבועי
אוג'
03
2011
קבצים מצורפים: היחידה כקובץ PDF, מצגת PPT
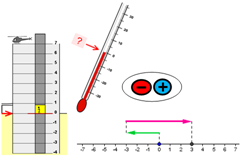
השוואה בין גורמים שונים היא חלק מחיי היומיום שלנו. במתמטיקה השוואות מתורגמות למשוואות ולאי-שוויונות המקבלים ייצוגים שונים: מילולי, גרפי, מספרי, ואלגברי.
בפתרון שאלה מילולית המתארת השוואה, נדרשת אוריינות מתמטית. הפותר צריך להבין את הנקרא, ולדעת לתרגם את התיאור המילולי לייצוג מתמטי אחר (גרפי, מספרי או אלגברי) אשר יוביל לתשובה.
התמודדות עם שאלות מילוליות המתארות אי-שוויון, דורשת הבנה של דקויות מילוליות. אוצר המונחים הלשוניים המתארים מצבי אי-שוויון רבים ומגוונים. ההבדלים הדקים בין מושגי האי-שוויון דורשים הבנה מעמיקה של הטקסט. למשל, המשפט "לדני יש 8 גולות לכל היותר" מתורגם ל-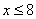 והמשפט "לדני יש יותר מ-8 גולות" מתורגם ל-
והמשפט "לדני יש יותר מ-8 גולות" מתורגם ל- 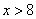 . ה"כיוון" של סימן האי-שוויון שונה וגם האי-שוויון הראשון הוא אי-שוויון חלש (מאפשר גם את השוויון עצמו) בעוד השני הוא אי-שוויון חזק (אינו מאפשר את השוויון עצמו).
. ה"כיוון" של סימן האי-שוויון שונה וגם האי-שוויון הראשון הוא אי-שוויון חלש (מאפשר גם את השוויון עצמו) בעוד השני הוא אי-שוויון חזק (אינו מאפשר את השוויון עצמו).
ביחידה זו נתמקד במשמעות הלוגית של אי-שוויון ובפתרון שאלות מילוליות המתארות אי-שוויון:
- נעסוק בדקויות ההבחנה בין המונחים המתארים אי-שוויונות.
- נבדיל בין מונחים המאפשרים שימוש באי-שוויון חלש או חזק.
- בפתרון השאלות נשתמש, במידת האפשר, בדרכים שונות ובייצוגים מגוונים.
אוג'
03
2011
או מדוע "מינוס כפול מינוס שווה פלוס"?
קבצים מצורפים: היחידה כקובץ PDF
פעולת הכפל במספרים השליליים היא פעולה המוגדרת באופן מתמטי פורמלי ולאו דוקא אינטואיטבי. זו אחת הפעולות הראשונות שפוגש התלמיד בבית הספר שמקורן אינו בהתנסויות מוחשיות ואינטואיטיביות. השרירותיות של החוקים המתמטיים מהווה לעיתים אבן נגף ברצף הלמידה של הרחבת המספרים וראשית האלגברה.
ביחידה זו נבחן הסברים שונים המקובלים בהוראה, בכדי להצדיק את חוקי הכפל במספרים השליליים ובפרט מדוע כפל של שני מספרים שליליים הוא חיובי. הצגת המספרים השליליים ופעולות החיבור והחיסור בהם נלמדות בדרך כלל בתווך של מודלים דידקטיים כגון חיצים על ציר המספרים, מודל האסימונים וכדומה (ראו סקירה נרחבת ביחידה "להיות מודל למספר שלילי"). ביחידה זו נשאל האם וכיצד נמשיך להשתמש במודלים להוראת פעולת הכפל במספרים שליליים וכן אילו אסטרטגיות מתאימות להצגת פעולת הכפל במספרים השליליים.
יחידה זו עוקבת ליחידה "להיות מודל למספר שלילי", אך יכולה לעמוד גם בפני עצמה.
אוג'
03
2011
מודלים שונים להצגת המספרים השליליים ופעולות החיבור והחיסור בהם
קבצים מצורפים: היחידה כקובץ PDF
היחידה עוסקת בחשיפה למודלים שונים המשמשים להוראת המספרים השלמים, השוואה בין המודלים השכיחים ובחינת המשמעות של המספר השלילי ופעולות החיבור והחיסור בכל אחד מהמודלים.
הנושאים המרכזיים
- הרחבת עולם המספרים.
- מספר שלילי – מהו?
- מושגים מרכזיים בהגדרת המספר השלילי – האפס, היחידה, נגדיות, סדר וצפיפות.
- ייצוגים שונים של המספרים השליליים במגוון מודלים דידקטיים.
- מה בין מושג ומודל?
- ארבע פעולות החשבון והמשמעות שלהן במודלים השונים.
- מקומם של המודלים בהוראה: נקודות חוזק ותורפה.
אוק'
12
2009
שלום לכולם
עוד הצעה לפעילות עם המורים בנושא חוקיות, או לפחות לחשוף את המורים לחומרים:
1. המאמר "מציאת חוקיות בדרך לאלגברה" מתוך העל"ה החדש.
2. הפיצוח "המלך מתיא חובב המתמטיקה" -הפיצוח עוסק בחוקיות, מציאת חוקים והכללות לתבניות גיאומטריות שונות כמבוא לאלגברה. הפיצוח מלווה ביישומים אינטראקטיביים שיסייעו בחקירה.
אגב, הפיצוח והפתרונות שלו מתורגמים לערבית!
3. מומלץ ביותר פעילויות אינטראקטיביות בנושא חוקיות:
משחק "חלצו את הפינגווין"
משחק הצפרדעים
לוח מספרים אינטראקטיבי
הפעילויות מלוות במדריך למורה.
ספט'
02
2009
הי לכולם ושתהיה שנה של בריאות ושלום והמון והמון מצויינות ומיצוי מקסימלי
לא ידעתי איך לצרף קובץ, הנה לכם יופי במתמטיקה שיכולים לשלב בנושא החוקיות
ולהרחיב קצת מעבר, אל החוכמת החיים (את המקור אני לא יודעת, קיבלתי במייל מחבר טוב):
היופי במתמטיקה!!!
1x 8 + 1 = 9
12x 8 + 2 = 98
123x 8 + 3 = 987
1234x 8 + 4 = 9876
12345x 8 + 5 = 98765
123456x 8 + 6 = 987654
1234567x 8 + 7 = 9876543
12345678x 8 + 8 = 98765432
123456789x 8 + 9 = 987654321
1x 9 + 2 = 11
12x 9 + 3 = 111
123x 9 + 4 = 1111
1234x 9 + 5 = 11111
12345x 9 + 6 = 111111
123456x 9 + 7 = 1111111
1234567x 9 + 8 = 11111111
12345678x 9 + 9 = 111111111
123456789x 9 +10= 1111111111
9x 9 + 7 = 88
98x 9 + 6 = 888
987x 9 + 5 = 8888
9876x 9 + 4 = 88888
98765x 9 + 3 = 888888
987654x 9 + 2 = 8888888
9876543x 9 + 1 = 88888888
98765432x 9 + 0 = 888888888
מבריק, לא?!
ותראו את הסמטריה כאן:
1x 1 = 1
11x 11 = 121
111x 111 = 12321
1111x 1111 = 1234321
11111x 11111 = 123454321
111111x 111111 = 12345654321
1111111x 1111111 = 1234567654321
11111111x 11111111 = 123456787654321
111111111x 111111111 = 12345678987654321
עכשיו תסתכלו על זה…
101%
לפי ההשקפה המתמטית:
מה שווה ל 100% ?
מה הכוונה ב"לתת יותר מ-100%" ?
תהייתם אי פעם באותם אנשים שאומרים "הם נתנו יותר מ- 100%" ?
אנחנו כל הזמן מגיעים למצבים שמישהו רוצה ש"ניתן יותר מ- 100%".
ומה בנוגע לביצוע של 101%?
מה שווה ערך ל 100% בחיינו?
זוהי נוסחה מתמטית קטנה שתוכל לעזור לך לענות על השאלות:
אם-
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
הם בעצם-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26.
אז:
K-N-O-W-L-E- D-G-E (ידע)
11+14+15+23+ 12+5+4+7+ 5 = 96%
ו:
H-A-R-D W-O- R- K (עבודה קשה)
8+1+18+4+23+ 15+18+11 = 98%
אבל
A-T-T-I-T-U- D-E (יחס)
1+20+20+9+20+ 21+4+5 = 100%
ותראה עד איפה האהבה של אלוהים יכולה לקחת אותך
L-O-V-E O-F G-O-D (אהבת אלוהים)
12+15+22+5+15+ 6+7+15+4 = 101%
לכן אפשר להסיק מהידע המתמטי הזה:
שעם עבודה קשה וידע תוכל להגיע קרוב למטרה,
אבל יחס יוכל לקחת אותך עד לשם.
וזאת אהבת אלוהים שתקח אותך מעבר לקצה!
אז תחלוק ידע זה עם חבריך ואהוביך בדרך שאני חלקתי איתם זאת…
המשך יום נעים
אוג'
13
2009
לפניכם מצגות וחומרים מתוך ההשתלמות:
פתרון שאלות מילוליות ברוח תכנית הלימודים החדשה במתמטיקה
השתלמות נערכה ע"י ניצה שיאון- מדריכה ארצית וד"ר מכאל פינקל- מדריך מחוזי ירושליים.
במצגות חומרים מתוך:
השתלמות "שאלות מילוליות" / ד"ר דוד פיילכנפלד
השתלמות "חשיבה מתמטית מהי?" / אגף שחר
חומרים בפיתוח מכון לטיפוח החשיבה ברנקו וויס
חומרים בפיתוח היחידה לחקר החינוך המתמטי באוניברסיטה העברית
חומרים בפיתוח המחלקה להוראת המדעים בטכניון
חומרים בפיתוח המחלקה להוראת המדעים במכון ויצמן למדע
- מצגת- תכנית הלימודים החדשה
- מצגת- שאלות מילוליות
- שאלות מילוליות
- שאלות מילוליות דוגמאות
- משימה אינטגרטיבית
- שאלות כדאיות- מועדון ספורט
- שפת האלגברה
- ניתוח נתונים איכותי
- שילוב תחומים